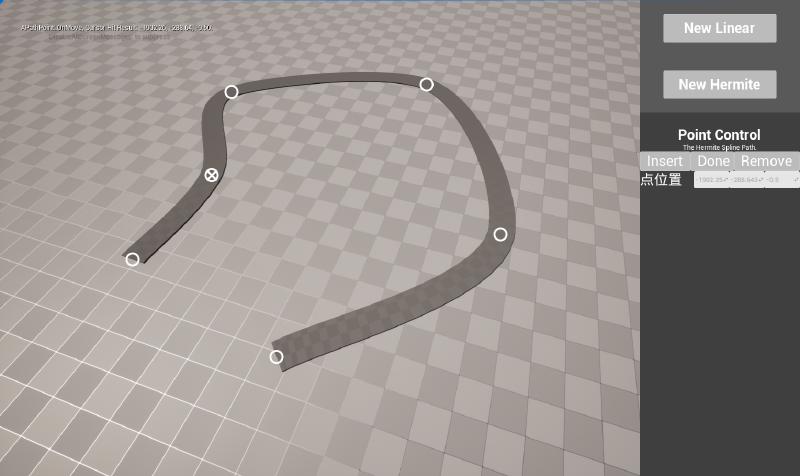
Hermite Spline
这是我最近学习样条的一篇笔记,关于Hermite Spline的知识来源主要来自维基百科,背景知识来自GAMES102。
常用的Hermite Spline一般指Cubic Hermite Spline,它与贝塞尔曲线同属于三次多项式样条(Cubic polynomial splines)。
三次多项式样条都是对于每两个控制点的小范围内生成插值曲线,连起来就是整条插值曲线。
Hermite样条生成的插值曲线是连续的,也经过所有的控制点。每个控制点需要包含位置向量(Position Vector)与正切向量(Tangent Vector)的信息。然而,在实际应用中,往往我们只是得到了确定的位置向量的信息,而正切向量则需要另外设置逻辑去估计。
插值公式
假设$t$的插值范围:$t\in [0,1]$。
起始点的位置与正切、终止点的位置与正切分别表示为$\overrightarrow{p}_k, \overrightarrow{m}_k, \overrightarrow{p}_{k+1}, \overrightarrow{m}_{k+1}$。
其中起始点的下标是$k$。
$$ \begin{aligned} \overrightarrow{p}(t)&=h_{00}(t)\overrightarrow{p}_k+h_{10}(t)\overrightarrow{m}_k+h_{01}(t)\overrightarrow{p}_{k+1}+h_{11}(t)\overrightarrow{m}_{k+1},\\ h_{00}(t)&=2t^3-3t^2+1,\\ h_{10}(t)&=t^3-2t^2+t,\\ h_{01}(t)&=-2t^3+3t^2,\\ h_{11}(t)&=t^3-t^2. \end{aligned} $$
其他范围的插值参数就把范围放缩到$[0,1]$即可。
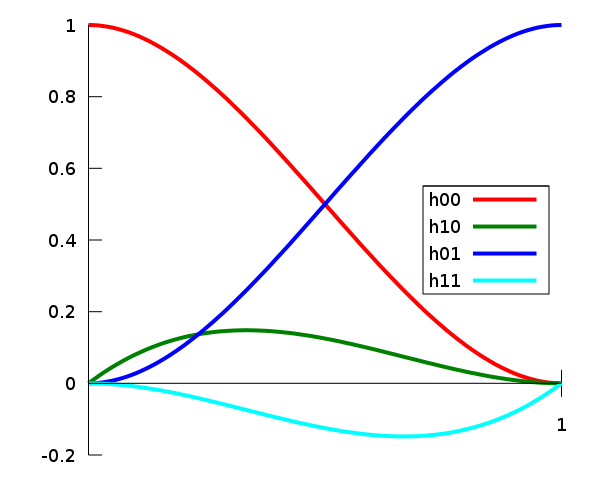
其中$h_{00}(t),h_{01}(t),h_{10}(t),h_{11}(t)$被称为Hermite基础函数(Hermite basis functions)。它们也可以表现成伯恩斯坦基的线性组合形式。
| expanded | factorized | Bernstein | |
|---|---|---|---|
| $h_{00}(t)$ | $2t^3-3t^2+1$ | $(1+2t)(1-t)^2$ | $B_0(t)+B_1(t)$ |
| $h_{10}(t)$ | $t^3-2t^2+t$ | $t(1-t)^2$ | $\cfrac13B_1(t)$ |
| $h_{01}(t)$ | $-2t^3+3t^2$ | $t^2(3-2t)$ | $B_3(t)+B_2(t)$ |
| $h_{11}(t)$ | $t^3-t^2$ | $t^2(t-1)$ | $-\cfrac13B_2(t)$ |
另外还可以将位置与正切作为系数,把这个三次多项式写成标准形式。
$$ \overrightarrow{p}(t)=(2\overrightarrow{p}_k+\overrightarrow{m}_k-2\overrightarrow{p}_{k+1}+\overrightarrow{m}_{k+1})t^3+(-3\overrightarrow{p}_k+3\overrightarrow{p}_{k+1}-2\overrightarrow{m}_k-\overrightarrow{m}_{k+1})t^2+\overrightarrow{m}_kt+\overrightarrow{p}_k. $$
这种形式在控制点相同、t值不同的多次计算中更有效率,因为系数可以计算一次并重复使用。
从控制点位置估计正切
合理地估计正切,是为了保证各段曲线组成的整条曲线在各个连接点都连续。而且它应该达到$C_2$连续,这样才能光滑。
估计正切的方法有很多种,维基百科里记录了几个常用的。
另外,有些时候t的取值并不在$[0,1]$,而是每两个控制点之间有任意长度的插值区间,那么就表示为$t\in[x_{k+1},x_k]$,两个控制点之间的长度就是$x_{k+1}-x_k$,当$k$取不同值时,$x_{k+1}-x_k$也可能不同,如果都相同,那么uniform parameter spacing,意思就是参数的间距是一样的。
Finite difference
$$ \overrightarrow{m}_k=\cfrac12(\cfrac{\overrightarrow{p}_{k+1}-\overrightarrow{p}_k}{x_{k+1}-x_k}+\cfrac{\overrightarrow{p}_{k}-\overrightarrow{p}_{k-1}}{x_{k}-x_{k-1}}). $$
有限差分不需要参数的间距都是一样的。
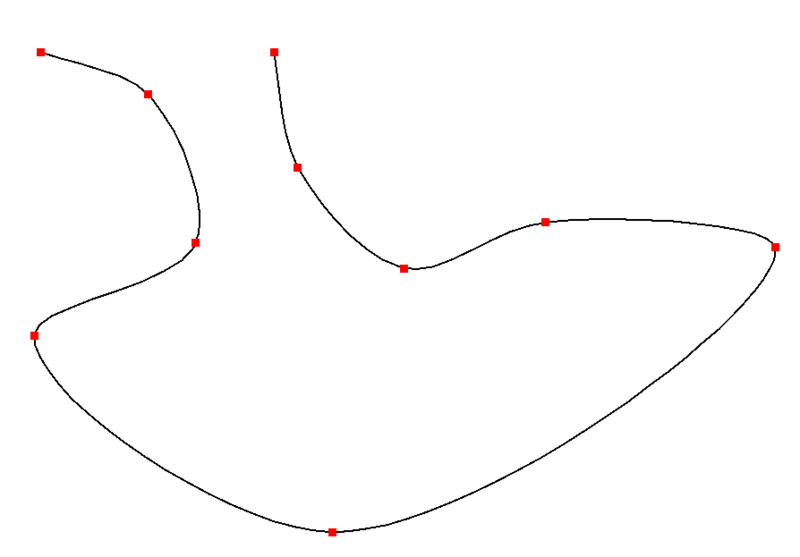
Cardinal spline
$$ \overrightarrow{m}_k=(1-c)\cfrac{\overrightarrow{p}_{k+1}-\overrightarrow{p}_{k-1}}{x_{k+1}-x_{k-1}} $$
其中$c\in[0,1]$,它叫tension parameter。在某种意义上,这可以解释为正切的“长度”。选择$c = 1$得到所有长度为0的正切,选择$c = 0$得到均匀参数化情况下的Catmull-Rom样条。听说可以通过改变$c$来控制曲线的形状,使得曲线更接近或远离控制点。

Catmull–Rom spline
这个我用得最多,它是cardinal spline的一个特例,这个简单的公式要求参数的间距都是一样的。
$$ \overrightarrow{m}_k=\cfrac{\overrightarrow{p}_{k+1}-\overrightarrow{p}_{k-1}}2 $$
这样实现出来的曲线可以是一个环路。Catmull-Rom样条经常用于在关键帧之间获得平滑的插值运动,它受欢迎的主要原因是相对容易计算,保证每个关键帧位置被准确击中,并保证生成的曲线的切线在多个段上连续。