使用欧拉角、球坐标旋转相机

最近折腾了一下相机跟随相关的功能，期间做了两个小玩具。一个是用欧拉角简单地让相机随鼠标旋转，另一个则是用球面坐标系的思路实现球形环绕相机，都是根据鼠标拖动来改变相机相对目标的姿态和位置。

欧拉角

当鼠标按下后，会先获取鼠标目前点击的世界坐标点作为旋转的中心点，同时记录相机当前的旋转矩阵和世界坐标位置，也记录相机到目标中心点的View Space位置差 OffsetHandle。 鼠标在移动时，每一帧都累计鼠标在 X、Y 方向的增量。 得到新的俯仰角和偏航角后，就能生成一个新的Delta旋转矩阵。 把OffsetHandle通过Delta旋转矩阵来旋转，得到新的View Space位置差，再把它变换回世界空间，就得到新的OffsetHandle， 再加上将相机应用上新的Delta旋转矩阵，就可以使得相机看起来随着鼠标沿着欧拉角旋转。

球坐标

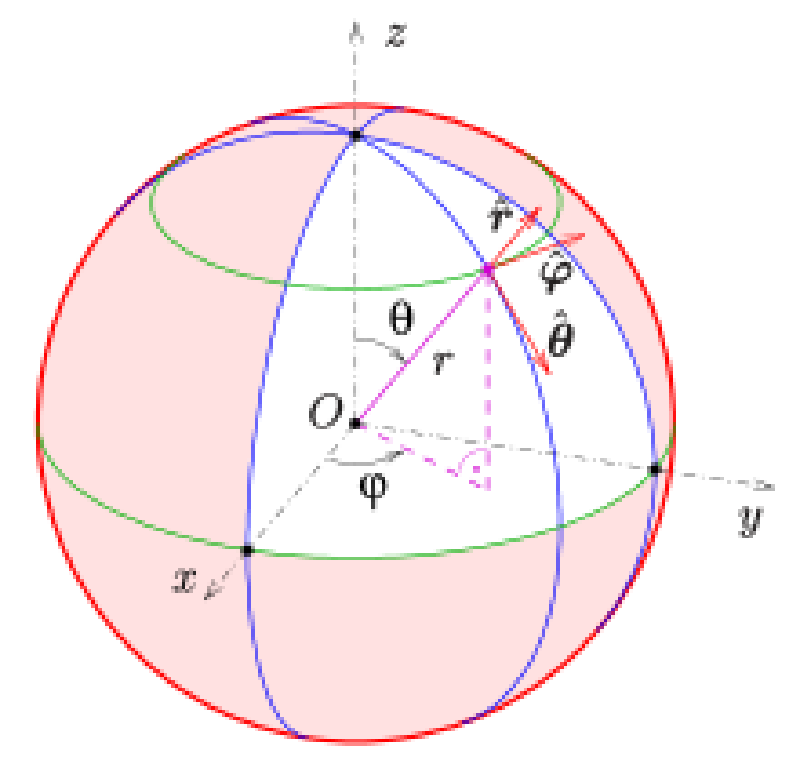
球形环绕的思路可以看作是欧拉角思路的进一步扩展，只不过不直接使用欧拉角来存储位置和旋转关系。 $$ x = r ⋅ sin(θ) ⋅ cos(φ)\ y = r ⋅ sin(θ) ⋅ sin(φ)\ z = r ⋅ cos(θ) $$ 由于实际代码中还要考虑到引擎世界坐标系的差异，所以最好在鼠标按下时，通过目标位置与点击点相减，就能得到当前相机在世界空间中的向量。进而求出对应的 r、θ、φ，并记住鼠标开始拖动时对应的“初始视图方向”。在每一次 Tick 中，根据鼠标移动增量更新 θ、φ，然后重新计算相机的坐标，再把它加回 LocationHandleRoot（即球心），就能让相机稳稳地保持在同一个球面半径上绕圈移动。

在代码中可以看到，FMath::Acos(LocationHandleFootRelative.Z / R) 就是对 θ 的求解，FMath::Atan2(LocationHandleFootRelative.Y, LocationHandleFootRelative.X) 则对 φ 做了求解。然后在更新相机位置后，再结合初始视图方向与新视图方向之间的夹角，通过四元数来进行细微纠正，以确保相机的朝向和我们期望的一致。此外，代码也做了夹角范围的限制，例如俯仰角 θ 被约束在 -89° 到 89° 之间，防止出现视角完全翻转的问题。

这种球坐标的好处就在于它比较容易做一些高级操作，例如流畅地实现绕目标旋转、限制上下视角以及只要修改 R 就能控制远近。此外，如果只需要简单绕固定轴旋转，那么欧拉角会更加直观一点。

Code: Euler

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

#include "Kismet/GameplayStatics.h"

constexpr float MinPitch = -89.0f;
constexpr float MaxPitch = 89.0f;

AEulerTester::AEulerTester()
{
	PrimaryActorTick.bCanEverTick = true;
}

void AEulerTester::Tick(float DeltaTime)
{
	Super::Tick(DeltaTime);

	if (PlayerController->IsInputKeyDown(EKeys::RightMouseButton))
	{
		if (!bIsDragging)
		{
			bIsDragging = true;
			FHitResult HitResult;
			if (!PlayerController->GetHitResultUnderCursor(ECC_Visibility, true, HitResult))
				return;
			LocationHandleRoot = HitResult.ImpactPoint;
			DrawDebugPoint(GetWorld(), LocationHandleRoot, 25.0f, FColor::White, false, 10.0f);

			RotationHandleFootStart = Pawn->GetActorRotation();
			FRotationMatrix CurrentRotationMatrix(RotationHandleFootStart);
			OffsetHandle = CurrentRotationMatrix.InverseTransformVector(Pawn->GetActorLocation() - LocationHandleRoot);
			YawDelta = 0.0f;
			PitchDelta = 0.0f;
		}
		else
		{
			float DeltaX, DeltaY;
			PlayerController->GetInputMouseDelta(DeltaX, DeltaY);

			constexpr float RotationSpeed = 1.0f;
			YawDelta += DeltaX * RotationSpeed;
			PitchDelta += DeltaY * RotationSpeed;
			FRotator NewRotation = RotationHandleFootStart;
			NewRotation.Yaw += YawDelta;
			NewRotation.Pitch += PitchDelta;

			FRotationMatrix RotMatrix{NewRotation};
			FVector NewOffset = RotMatrix.TransformVector(OffsetHandle);
			FVector NewLocation = LocationHandleRoot + NewOffset;
			Pawn->SetActorLocation(NewLocation);
			Pawn->SetActorRotation(NewRotation);

			DrawDebugPoint(GetWorld(), LocationHandleRoot, 15.0f, FColor::Red, false, -1.0f);
			DrawDebugLine(GetWorld(), LocationHandleRoot, Pawn->GetActorLocation(), FColor::Green, false, -1.0f);

			FVector CameraForward = Pawn->GetActorForwardVector() * 100.0f;
			DrawDebugLine(GetWorld(), Pawn->GetActorLocation(),
			              Pawn->GetActorLocation() + CameraForward,
			              FColor::Blue, false, -1.0f);
		}
	}
	else
	{
		bIsDragging = false;
	}
}

void AEulerTester::BeginPlay()
{
	Super::BeginPlay();

	PlayerController = UGameplayStatics::GetPlayerController(GetWorld(), 0);
	PlayerController->SetShowMouseCursor(true);
	FInputModeGameAndUI InputModeGameAndUI;
	InputModeGameAndUI.SetLockMouseToViewportBehavior(EMouseLockMode::DoNotLock);
	PlayerController->SetInputMode(InputModeGameAndUI);
	Pawn = PlayerController->GetPawn();
}

Code: Spherical

r::Tick(float DeltaTime) { Super::Tick(DeltaTime);

if (PlayerController->IsInputKeyDown(EKeys::RightMouseButton))
{
	if (!bIsDragging)
	{
		bIsDragging = true;
		FHitResult HitResult;
		PlayerController->GetHitResultUnderCursor(ECC_Visibility, true, HitResult);
		LocationHandleRoot = HitResult.ImpactPoint;
		LocationHandleFootRelative = Pawn->GetActorLocation() - LocationHandleRoot;
		R = LocationHandleFootRelative.Length();
		Theta = FMath::Acos(LocationHandleFootRelative.Z / R);
		Phi = FMath::Atan2(LocationHandleFootRelative.Y, LocationHandleFootRelative.X);

		FMatrix ViewMatrix = FRotationMatrix(Pawn->GetActorRotation());
		PositionInitialView = ViewMatrix.InverseTransformVector(-LocationHandleFootRelative);
	}
	else
	{
		float DeltaX, DeltaY;
		PlayerController->GetInputMouseDelta(DeltaX, DeltaY);
		constexpr float RotationSpeed = .5f;
		Theta = FMath::ClampAngle(Theta + DeltaY * DeltaTime * RotationSpeed, MinPitch, MaxPitch);
		Phi += DeltaX * DeltaTime * RotationSpeed;
		LocationHandleFootRelative = {
			R * FMath::Sin(Theta) * FMath::Cos(Phi),
			R * FMath::Sin(Theta) * FMath::Sin(Phi),
			R * FMath::Cos(Theta)
		};
		Pawn->SetActorLocation(LocationHandleRoot + LocationHandleFootRelative);

		FRotator BaseRotation = (-LocationHandleFootRelative).Rotation();
		FMatrix NewViewMatrix = FRotationMatrix(BaseRotation);
		FVector CurrentViewDir = NewViewMatrix.
			InverseTransformVector(LocationHandleRoot - Pawn->GetActorLocation());
		FQuat CorrectionQuat = FQuat::FindBetweenVectors(PositionInitialView, CurrentViewDir);
		FRotator FinalRotation = (BaseRotation.Quaternion() * CorrectionQuat).Rotator();
		Pawn->SetActorRotation(FinalRotation);
	}
}
else
{
	bIsDragging = false;
}

if (bIsDragging)
{
	DrawDebugPoint(GetWorld(), LocationHandleRoot, 10.0f, FColor::Red, false, -1.0f);
	DrawDebugLine(GetWorld(), LocationHandleRoot, Pawn->GetActorLocation(), FColor::Green, false, -1.0f);

	FVector CameraForward = Pawn->GetActorForwardVector() * 100.0f;
	DrawDebugLine(GetWorld(), Pawn->GetActorLocation(),
	              Pawn->GetActorLocation() + CameraForward,
	              FColor::Blue, false, -1.0f);
}

}

void ASphereTester::BeginPlay() { Super::BeginPlay();

PlayerController = UGameplayStatics::GetPlayerController(GetWorld(), 0);
PlayerController->SetShowMouseCursor(true);
FInputModeGameAndUI InputModeGameAndUI;
InputModeGameAndUI.SetLockMouseToViewportBehavior(EMouseLockMode::DoNotLock);
PlayerController->SetInputMode(InputModeGameAndUI);
Pawn = PlayerController->GetPawn();

}