Moving Camera Using Euler or Spherical Coordinates
Recently, I’ve been tinkering with camera follow functionalities and created two small “toys” in the process. One uses Euler angles to simply rotate the camera based on mouse movements, and the other implements a spherical orbiting camera using spherical coordinate system principles. Both modify the camera’s pose and position relative to a target based on mouse dragging.
Euler Angles
When the mouse is pressed down, the world coordinate point where the mouse clicked is first obtained as the center of rotation. At the same time, the camera’s current rotation matrix, world coordinate position, and the View Space position difference (OffsetHandle) between the camera and the target’s center point are also recorded.
As the mouse moves, the incremental changes in the X and Y directions of the mouse are accumulated each frame.
After obtaining the new pitch and yaw angles, a new Delta rotation matrix can be generated.
The OffsetHandle is rotated using the Delta rotation matrix to obtain a new View Space position difference. This is then transformed back into world space to get the new OffsetHandle.
Applying the new Delta rotation matrix to the camera itself makes the camera appear to rotate along the Euler angles with the mouse.
Spherical Coordinates
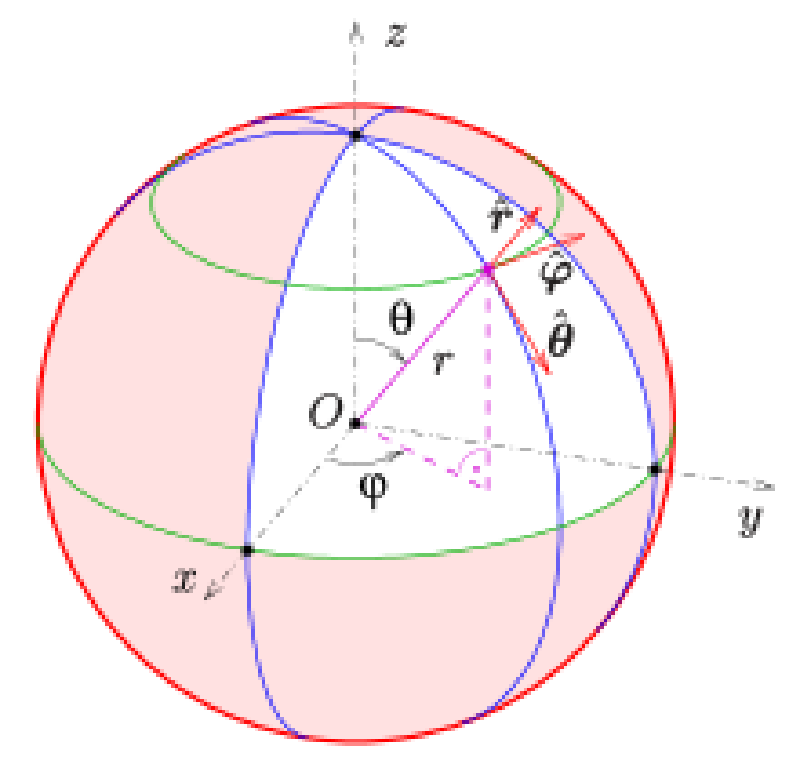
The spherical orbiting approach can be seen as a further extension of the Euler angle approach, except that Euler angles are not directly used to store the position and rotation relationship.
$$ x = r ⋅ sin(θ) ⋅ cos(φ) y = r ⋅ sin(θ) ⋅ sin(φ) z = r ⋅ cos(θ) $$
Because actual code has to consider the differences in the engine’s world coordinate system, it’s best to subtract the target position from the click point when the mouse is pressed down to obtain the current camera’s vector in world space. From this, the corresponding r, θ, and φ can be calculated, and the corresponding “initial view direction” when the mouse starts dragging is remembered. In each Tick, update θ and φ based on the mouse movement increments, then recalculate the camera’s coordinates, and add it back to LocationHandleRoot (i.e., the center of the sphere). This allows the camera to stably maintain its position on the same spherical radius while orbiting.
In the code, FMath::Acos(LocationHandleFootRelative.Z / R) is the solution for θ, and FMath::Atan2(LocationHandleFootRelative.Y, LocationHandleFootRelative.X) performs the solution for φ. After updating the camera position, the angle between the initial view direction and the new view direction is combined, and quaternions are used for fine-tuning correction to ensure that the camera’s orientation is consistent with our expectations. In addition, the code also limits the angle range, such as constraining the pitch angle θ between -89° and 89° to prevent the issue of completely flipping the viewpoint.
The advantage of this spherical coordinate approach is that it’s easier to implement some advanced operations, such as smoothly rotating around the target, limiting the up and down view angles, and controlling the zoom simply by modifying R. Furthermore, if only simple rotation around a fixed axis is required, Euler angles are more intuitive.
Code: Euler
|
|
Code: Spherical
r::Tick(float DeltaTime) { Super::Tick(DeltaTime);
if (PlayerController->IsInputKeyDown(EKeys::RightMouseButton))
{
if (!bIsDragging)
{
bIsDragging = true;
FHitResult HitResult;
PlayerController->GetHitResultUnderCursor(ECC_Visibility, true, HitResult);
LocationHandleRoot = HitResult.ImpactPoint;
LocationHandleFootRelative = Pawn->GetActorLocation() - LocationHandleRoot;
R = LocationHandleFootRelative.Length();
Theta = FMath::Acos(LocationHandleFootRelative.Z / R);
Phi = FMath::Atan2(LocationHandleFootRelative.Y, LocationHandleFootRelative.X);
FMatrix ViewMatrix = FRotationMatrix(Pawn->GetActorRotation());
PositionInitialView = ViewMatrix.InverseTransformVector(-LocationHandleFootRelative);
}
else
{
float DeltaX, DeltaY;
PlayerController->GetInputMouseDelta(DeltaX, DeltaY);
constexpr float RotationSpeed = .5f;
Theta = FMath::ClampAngle(Theta + DeltaY * DeltaTime * RotationSpeed, MinPitch, MaxPitch);
Phi += DeltaX * DeltaTime * RotationSpeed;
LocationHandleFootRelative = {
R * FMath::Sin(Theta) * FMath::Cos(Phi),
R * FMath::Sin(Theta) * FMath::Sin(Phi),
R * FMath::Cos(Theta)
};
Pawn->SetActorLocation(LocationHandleRoot + LocationHandleFootRelative);
FRotator BaseRotation = (-LocationHandleFootRelative).Rotation();
FMatrix NewViewMatrix = FRotationMatrix(BaseRotation);
FVector CurrentViewDir = NewViewMatrix.
InverseTransformVector(LocationHandleRoot - Pawn->GetActorLocation());
FQuat CorrectionQuat = FQuat::FindBetweenVectors(PositionInitialView, CurrentViewDir);
FRotator FinalRotation = (BaseRotation.Quaternion() * CorrectionQuat).Rotator();
Pawn->SetActorRotation(FinalRotation);
}
}
else
{
bIsDragging = false;
}
if (bIsDragging)
{
DrawDebugPoint(GetWorld(), LocationHandleRoot, 10.0f, FColor::Red, false, -1.0f);
DrawDebugLine(GetWorld(), LocationHandleRoot, Pawn->GetActorLocation(), FColor::Green, false, -1.0f);
FVector CameraForward = Pawn->GetActorForwardVector() * 100.0f;
DrawDebugLine(GetWorld(), Pawn->GetActorLocation(),
Pawn->GetActorLocation() + CameraForward,
FColor::Blue, false, -1.0f);
}
}
void ASphereTester::BeginPlay() { Super::BeginPlay();
PlayerController = UGameplayStatics::GetPlayerController(GetWorld(), 0);
PlayerController->SetShowMouseCursor(true);
FInputModeGameAndUI InputModeGameAndUI;
InputModeGameAndUI.SetLockMouseToViewportBehavior(EMouseLockMode::DoNotLock);
PlayerController->SetInputMode(InputModeGameAndUI);
Pawn = PlayerController->GetPawn();
}
|
|